| Auteur |
 Sujet  |
|
|
Marc 75017
Pilier de forums
2496 réponses |
 Posté - 20 mars 2005 : 16:16:21
|
Et, pour en revenir au tore, regardez ce qui se passe lorsque le tore se tue en se mettant à glubser comme un gros kon de ouf en justement s’enfilant tout seul un truc bleu qu'il tire de sa propre panse sans faire trop gaffe :
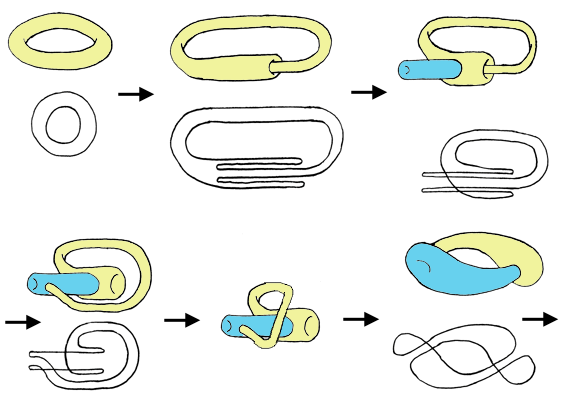
Remarquez, c’est peut être mieux que le tore qui se fait des super gros sacs de nœuds noués graves comak comme le ferait une bande de trente six paires de oufs :
Marc |
Edité par - Marc 75017 le 20 mars 2005 16:17:20 |
Signaler un abus  |
|
|
Lo_
Pilier de forums
3209 réponses |
Posté - 20 mars 2005 : 16:38:35
|
Le 1er (animé) on dirait ce que l’on voit dans un kaléidoscope... c'est vrai que lorsque les bleus apparaissent... c'est vraiment agréable à l'oeil...
Le 2eme, si l’on ôte les flèches, on pourrait croire une esquisse de Miro ou Klee…
Le 3eme, on dirait une bague posée…
C’est tout simplement joli…
Lo |
Edité par - Lo_ le 20 mars 2005 16:39:18 |
| Signaler un abus |
|
|
Lo_
Pilier de forums
3209 réponses |
|
|
Marc 75017
Pilier de forums
2496 réponses |
Posté - 21 mars 2005 : 04:35:44
|
Allez, de plus en plus fort : un sac de noeuds de bandes de Moebius
Marc |
Edité par - Marc 75017 le 21 mars 2005 04:47:32 |
| Signaler un abus |
|
|
Lo_
Pilier de forums
3209 réponses |
|
|
Marc 75017
Pilier de forums
2496 réponses |
Posté - 21 mars 2005 : 14:27:00
|
Oui, mais attention parce que si tout est bleu, fait des nœuds et s’emmêle, ça peut mal se finir :
Marc |
| Signaler un abus |
|
|
Lo_
Pilier de forums
3209 réponses |
|
|
Marc 75017
Pilier de forums
2496 réponses |
|
|
Lo_
Pilier de forums
3209 réponses |
Posté - 21 mars 2005 : 15:36:10
|
Et celui là ????
… N’en n’est pas un, mais n’en n’est pas pour autant inintéressant…
^^
Lo |
| Signaler un abus |
|
|
Lo_
Pilier de forums
3209 réponses |
Posté - 21 mars 2005 : 15:41:20
|
Oui, mais attention parce que si tout est bleu, fait des nœuds et s’emmêle, ça peut mal se finir :
… ça finira mal uniquement s’il prend la grosse tête (elle ne passera plus dans l’anneau) sinon, aucun souci que la fin soit tristement définitive…
^^
Lo |
| Signaler un abus |
|
|
Lo_
Pilier de forums
3209 réponses |
|
|
Lo_
Pilier de forums
3209 réponses |
|
|
Lo_
Pilier de forums
3209 réponses |
Posté - 02 juin 2005 : 23:13:43
|
Je viens de trouver une représentation du ruban de Moebius … sous forme de bijou…
La devise gravée : "L'anneau de Moebius, un infini mystérieux"
Lo |
| Signaler un abus |
|
|
Marc 75017
Pilier de forums
2496 réponses |
Posté - 04 juin 2005 : 00:52:06
|
Avec cette revivification inattendue et magique de ce sujet, et compte tenu de la tournure que vous y introduisez maintenant, je crois qu’il est vraiment temps de donner le lien sur le forum de maths-forum.com où l’on ira chercher le sujet « Séries de Lambert et fonction de Moebius » : http://www.maths-forum.com/entraide-mathematique-f6_7/ . Il y a toujours des sinus et des cosinus qui coincent ou dérapent dans les tournants, car ils n'arrivent pas à prendre la tangente...
Marc |
Edité par - Marc 75017 le 04 juin 2005 00:52:42 |
| Signaler un abus |
|
|
Lo_
Pilier de forums
3209 réponses |
Posté - 04 juin 2005 : 04:58:24
|
En période de révisions.... ça peut toujours servir...
Lo |
| Signaler un abus |
|
|
Sujet |
|
|
joint torique !!!!
Forum fermé
